Intro

Wanting to streamline and automate actions relating to derivatives trading I sought out to find a calculator library I could wrap an API around to calculate various outcomes.

A derivative is a contract between two or more parties whose value is based on an agreed-upon underlying financial asset, index or security.

Sadly I found nothing suitable or simple, so I implemented my own called guant using the Black-Scholes pricing model and Newton-Raphson model.

Considerations

Derivatives come in many forms and thus have many different associated formulas.

In this case we’ll be focusing on Options Contracts, so lets take a look at the related formulas.

1. Black-Scholes pricing model
2. Binomial options pricing model
3. Trinomial options pricing model
4. Bjerksund-Stensland Model

Black-Scholes is often used to price European options that can only be exercised on their expiry date, and without consideration to dividends.

The other 3 models take into account both of those factors and more to come up with a higher degree of accuracy when pricing American options.

After much reading on the topic I came across this quant stack exchange article explaining why Black-Scholes is still used as the benchmark, so we’ll implement this model.

Calculating implied volatility has it’s own considerations but we’ll address that specifically later.

Implementation of Black-Scholes

Between Investopedia, Wikipedia, and Khan Academy it’s clear what needs to be done.

After watching Khan work through the formula we just need to transfer the following into code.

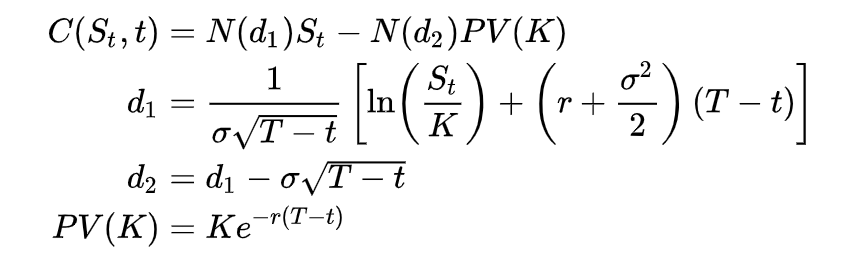
The core of our implementation comes out to these few functions alongside some other helpers for certain values such as time.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

func (a *Asset) d1() float64 {
	return (math.Log(a.S/a.K) + ((a.R + (a.Sigma*a.Sigma)/2) * a.T)) / (a.Sigma * math.Sqrt(a.T))
}

func (a *Asset) d2() float64 {
	return (math.Log(a.S/a.K) + ((a.R - (a.Sigma*a.Sigma)/2) * a.T)) / (a.Sigma * math.Sqrt(a.T))
}

func blackScholesCall(a Asset) float64 {
	return ((a.S * a.N.CDF(a.d1())) - ((a.K * math.Exp(-a.R*a.T)) * a.N.CDF(a.d2())))
}

func blackScholesPut(a Asset) float64 {
	return ((a.N.CDF(-1*a.d2()) * (a.K * math.Exp(-a.R*a.T))) - (a.S * a.N.CDF(-1*a.d1())))
}

Implementation of Newton-Raphson

An important part of pricing options is knowing their Sigma or Implied Volatility(IV). We can calculate IV with the current option and underlying price. This is useful as it will allow us to nice solve for the option at various underlying prices and times. IV is not a constant, it is an approximation and as such liable to change. We can compensate for this by avoiding buying options at higher implied volatilities or too close to events such as earnings.

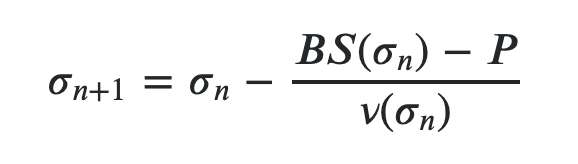
With this method we choose a starting value for Sigma and iteratively calculate using the option value and underlying price until it converges. This results in a high degree of accuracy.

There are more nuanced approaches we can use such as implementing a closed form solution or secant method and then iterating on that to achieve a higher degree of accuracy.

This youtuber had a pretty solid breakdown of using Newton’s Method so in the interest of being simple but effective we’ll implement the same way.

Pulling it all together

By combining guant with the go-finance library we can pull options contract values and current stock quotes to calculate options value for a given strike/expiry on a ticker.

We’ll use a Microsft Call Option with a Strike of $190 and an expiry of 2020-06-05.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

func main() {
	//Initial declarations
	ticker := "MSFT"
	var strike float64 = 190.00
	expiry := "2020-06-05"
	t := guant.TimeToExpiry(expiry)

	//Get current price
	q, err := quote.Get(ticker)
	if err != nil {
		panic(err)
	}
	currPrice := q.RegularMarketPrice

	//Get option data
	e, err := time.Parse("2006-01-02", expiry)
	if err != nil {
		fmt.Errorf("could not parse expiration- correct format is yyyy-mm-dd")
	}
	p := &options.Params{
		UnderlyingSymbol: ticker,
		Expiration:       datetime.New(&e),
	}

	// Iterate through list of options to find the value of the Call at our Strike/Expiry
	var mid float64 = 0
	iter := options.GetStraddleP(p)
	for iter.Next() {
		if iter.Straddle().Call != nil {
			if iter.Straddle().Call.Strike == strike {
				mid = (iter.Straddle().Call.Ask + iter.Straddle().Call.Bid) / 2
			}
		}
	}
	//To calculate the IV we'll use the options mid contract price from go-finance (Yahoo)
	// By calculating the IV we can use the IV then to calculate profit at other underlying Price values
	x := guant.Asset{
		N: distuv.Normal{Mu: 0, Sigma: 1},
		S: currPrice,
		K: strike,
		R: guant.DefaultRfir(),
		T: t,
	}
	sigma := guant.NewtonRaphson(x, mid)
	x.Sigma = sigma
	contractValue := guant.BlackScholes(x)


	fmt.Printf("Call Option Contract: %s -- %s -- Strike Price: %.2f\n", ticker, expiry, strike)
	fmt.Println("Current Price:", currPrice)
	fmt.Println("Calculated IV:", x.Sigma)
	fmt.Printf("Black-Scholes Call option Price : %.2f\n", contractValue)
}

Conclusion

The results from implementing guant and running the calculation come out as follows:

For comparison here is the same options contract listed on Robinhood.

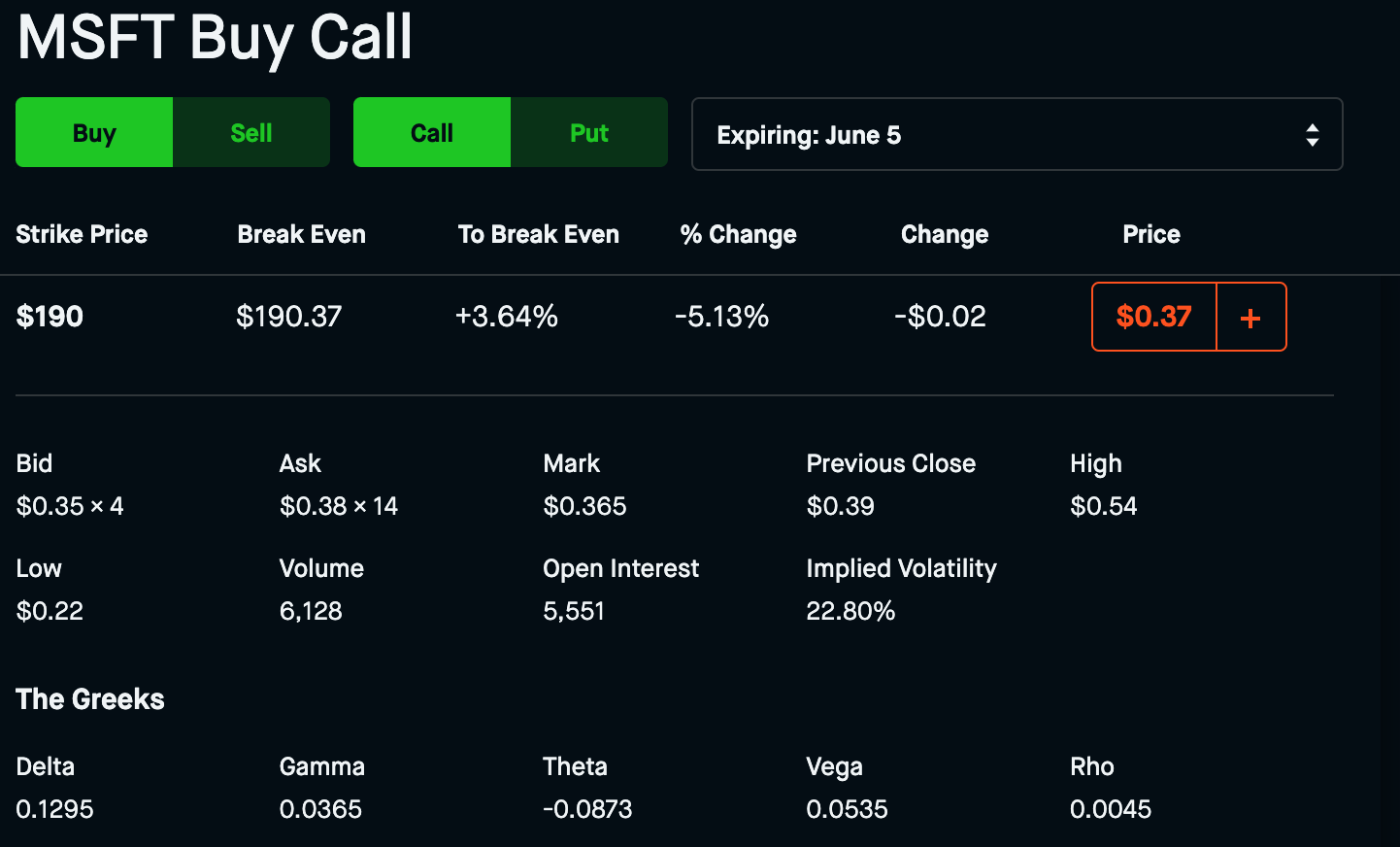
We’ll notice that our IV is incredibly close to Robinhoods IV, along with the value of the Call option.

It’s worth noting that these formulas yield approximations, the ultimate value of the contract is determined by the market. Hence the difference between the Bid and Ask prices.

Of course theres always ways to improve the results, one such easy addition may be making the time input more granular.

This has been a fun journey into the world of Quantitative finance and learning about some of the underlying mechanisms in derivatives.

Disclaimer for anyone who decides to use this, it is not guranteed at all to be reliable or accurate.